We are interested in an asynchronous graph based model, \(\boldsymbol {\mathcal {G}(N,E)}\) of cognition or cognitive dysfunction, where the nodes N provide computation at the neuron level and the edges Ei→j between nodes Ni and node Nj specify internode calculation.
Methods
We discuss how to improve update and evaluation needs for fast calculation using approximations of neural processing for first and second messenger systems as well as the axonal pulse of a neuron.
Results
These approximations give rise to a low memory footprint profile for implementation on multicore platforms using functional programming languages such as Erlang, Clojure and Haskell when we have no shared memory and all states are immutable.
Conclusions
The implementation of cognitive models using these tools on such platforms will allow the possibility of fully realizable lesion and longitudinal studies.
Keywords
Cognition modelsGraphs of computational nodesNodal computation approximation
Background
We note all brain models connect computational nodes (typically neurons) to other computational nodes using edges between the nodes. The proper background and motivation for this approach are discussed in (Peterson 2014a). That review article provides a reasonable introduction to the blend of ideas from mathematics, biophysics and signaling theory such as first and second messengers along with neurobiological concepts and computational implementation issues that are the foundation for the work presented here. We intend this article for researchers from computational, biological and mathematical backgrounds and the review provides an overview and a common set of notations and language. On the basis of that background material, we therefore model the neural circuitry of a brain using a directed graph architecture \(\boldsymbol {\mathcal {G}(N,E)}\) consisting of computational nodes N and edge functions E which mediate the transfer of information between two nodes. Hence, if Ni and Nj are two computational nodes, then Ei→j would be the corresponding edge function that handles information transfer from node Ni and node Nj. We organize the directed graph using interactions between neural modules (visual cortex, thalamus etc) which are themselves subgraphs of the entire circuit. Once a direct graph is chosen to represent neural circuitry, the addition of new neural modules is easily handled as a subgraph addition. Although connectivity is time dependent, we can think of a useful brain model as a sequence of such graphs of nodes and edges. For simulation purposes, this means there is a finite sequence of times, {t1,t2,…,tn} and associated graphs \(\boldsymbol {\mathcal {G}_{i}(N_{i},E_{i})}\), where the subscript i denotes the time point ti. In between these times, the graph has fixed connectivity and we can use a variety of tools to train the graph to meet input to output objectives. At each time point, we can therefore build our cognitive model using many different approaches as detailed in, e.g. (Friston 2005, 2010; Russo and Nestler 2013; Sherman 2004) and (Maia and Frank 2011). Indeed, some topology considerations for schizophrenia are directly addressed in (Li et al. 2012). However, here we are concerned with how to approximate the details of nodal processing so that computations can be performed efficiently with low memory footprint using the no shared memory model of a functional programming language such as Erlang, Haskell and Clojure. These languages allow us to design simple processes that interact and have no shared memory state. On even a typical laptop today, we can have four cores and 16 GB of memory, so it is easily possible to simulate the interactions of many thousands of simple interacting neurons as simple processes. Recall in the graph context, the update equations for a given node then are given as an input/output pair. For the node Ni, let yi and Yi denote the input and output from the node, respectively. Then we have
where Ii is a possible external input, \(\boldsymbol {\mathcal B}(i)\) is the list of nodes which connect to the input side of node Ni and σi(t) is the function which processes the inputs to the node into outputs. This processing function is mutable over time t because second messenger systems are altering how information is processing each time tick. Hence, our model consists of a graph
which captures the connectivity or topology of the brain model on top of which is laid the instructions for information processing via the time dependent node and edge processing functions. A simple look at edge processing shows the nodal output which is perhaps an action potential which is transferred without change to a synaptic connection where it initiates a spike in Ca+2 ions which results in neurotransmitter release. The efficacy of this release depends on many things, but we can focus on four: ru(i,j), the rate of re-uptake of neurotransmitter in the connection between node Ni and node Nj; the neurotransmitter is destroyed via an appropriate oxidase at the rate rd(i,j); the rate of neurotransmitter release, rr(i,j) and the density of the neurotransmitter receptor, nd(i,j). The triple (ru(i,j),rd(i,j),rr(i,j))≡T(i,j) determines a net increase or decrease of neurotransmitter concentration between the two nodes: rr(i,j)−ru(i,j)−rd(i,j)≡rnet(i,j). The efficacy of a connection between nodes is then proportional to the product Wi,j=rnet(i,j)×nd(i,j). Hence, each triple is a determining signature for a given neurotransmitter and the effectiveness of the neurotransmitter is proportional to the new neurotransmitter flow times the available receptor density. A very simple version of this is to simply assign the value of the edge processing function Ej→i to be the weight Wi,j as is standard in a simple connectionist architecture. We want to be more sophisticated than this and therefore want to allow our nodal processing functions to approximate the effects of both first and second messenger systems; consult (Peterson 2014a) for more detail.
Cellular triggers
Now consider the transcriptional control of a regulatory molecule such as NFκB (which plays a role in immune system response) or a neurotransmitter. We can call this a trigger and denote it by T0. This mechanism is discussed in a semi-abstract way in (Gerhart and Kirschner 1997); we will discuss even more abstractly. Consider a trigger T0 which activates a cell surface receptor. Inside the cell, there are always protein kinases that can be activated in a variety of ways. Here we denote a protein kinase by the symbol PK. A common mechanism for such an activation is to add to PK another protein subunit
to form the complex
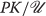. This chain of events looks like this:
where CSR denotes a cell surface receptor.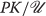
then acts to phosphorylate another protein. The cell is filled with large amounts of a transcription factor we will denote by T1 and an inhibitory protein for T1 we label as \(T_{1}^{\sim }\). This symbol, \(T_{1}^{\sim }\), denotes the complement or anti version of T1. In the cell, T1 and \(T_{1}^{\sim }\) are generally joined together in a complex denoted by \(T_{1}/T_{1}^{\sim }\). The addition of \(T_{1}^{\sim }\) to T1 prevents T1 from being able to access the genome in the nucleus to transcribe its target protein.
The trigger T0 activates our protein kinase PK to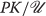
. The activated
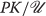is used to add a phosphate to \(T_{1}^{\sim }\). This is called phosphorylation. Hence,
where \(T_{1}^{\sim } P\) denotes the phosphorylated version of \(T_{1}^{\sim }\). Since T1 is bound into the complex \(T_{1}/T_{1}^{\sim }\), we actually have
In the cell, there is always present a collection of proteins which tend to bond with the phosphorylated form \(T_{1}^{\sim } P\). Such a system is called a tagging system. The protein used by the tagging system is denoted by
and usually a chain of n such
proteins is glued together to form a polymer
. The tagging system creates the new complex
. This gives the following event tree at this point:
Also, inside the cell, the tagging system coexists with a complimentary system whose function is to destroy or remove the tagged complexes. Hence, the combined system \(\text {Tag} \leftarrow \rightarrow \text {Remove} \: \rightarrow \: T_{1}/T_{1}^{\sim } P\) is a regulatory mechanism which allows the transcription factor T1 to be freed from its bound state \(T_{1}/T_{1}^{\sim }\) so that it can perform its function of protein transcription in the genome. The removal system is specific to
molecules; hence although it functions on
, it would work just as well on
where Q is any other tagged protein. We will denote the removal system which destroys
tagged proteins Q from a substrate S by the symbol
. This symbol means the system acts on
units and outputs S via mechanism f. Note the details of the mechanism f are largely irrelevant here. Thus, we have the reaction
which releases T1 into the cytoplasm. The full event chain is thus:
where N is the nucleus, TPT denotes the phrase tagged protein transcription and P(T1) indicates the protein whose construction is initiated by the trigger T0. Without the trigger, we see there are a variety of ways transcription can be stopped:
T1 does not exist in a free state; instead, it is always bound into the complex \(T_{1}/ T_{1}^{\sim }\) and hence can’t be activated until the \(T_{1}^{\sim }\) is removed.
Any of the steps required to remove \(T_{1}^{\sim }\) can be blocked effectively killing transcription:
phosphorylation of \(T_{1}^{\sim }\) into \(T_{1}^{\sim } P\) is needed so that tagging can occur. So anything that blocks the phosphorylation step will also block transcription.
Anything that blocks the tagging of the phosphorylated \(T_{1}^{\sim } P\) will thus block transcription.
Anything that stops the removal mechanism
will also block transcription.
The steps above can be used therefore to further regulate the transcription of T1 into the protein P(T1). Let \(T_{0}^{\prime }\), \(T_{0}^{\prime \prime }\) and \(T_{0}^{\prime \prime \prime }\) be inhibitors of the steps above. These inhibitory proteins can themselves be regulated via triggers through mechanisms just like the ones we are discussing. In fact, P(T1) could itself serve as an inhibitory trigger - i.e. as any one of the inhibitors \(T_{0}^{\prime }\), \(T_{0}^{\prime \prime }\) and \(T_{0}^{\prime \prime \prime }\). Our theoretical pathway is now:
where the step i, step ii and step iii can be inhibited as shown below:
Note we have expanded to a system of four triggers which effect the outcome of P(T1). Also, note that step i is a phosphorylation step. Now, let’s refine our analysis a bit more. Usually, reactions are paired: we typically have the competing reactions
Hence, we can imagine that step i is a system which is in dynamic equilibrium. The amount of \(T_{1}/T_{1}^{\sim } P\) formed and destroyed forms a stable loop with no net \(T_{1}/T_{1}^{\sim } P\) formed. The trigger T0 introduces additional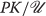
into this stable loop and thereby effects the net production of \(T_{1}/T_{1}^{\sim } P\). Thus, a new trigger \(T_{0}^{\prime }\) could profoundly effect phosphorylation of \(T_{1}^{\sim }\) and hence production of P(T1). We can see from the above comments that very fine control of P(T1) production can be achieved if we think of each step as a dynamical system in flux equilibrium. Note our discussion above is a first step towards thinking of this mechanism in terms of interacting objects.
Dynamical loop details
Our dynamical loop consists of the coupled reactions
where k1 and k−1 are the forward and backward reaction rate constants and we assume the amount of \(T_{1}/T_{1}^{\sim }\) inside the cell is constant and maintained at the equilibrium concentration \(\left [T_{1}/T_{1}^{\sim }\right ]_{e}\). Since one unit of
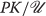combines with one unit of \(T_{1}/T_{1}^{\sim }\) to phosphorylate \(T_{1}/T_{1}^{\sim }\) to \(T_{1}/T_{1}^{\sim } P\), we see
(1)
Hence,
. For this reaction, we have
; thus, we find
Hence, at equilibrium, \(\frac {d[T_{1}/T_{1}^{\sim }]}{dt} = 0\) implying
(4)
Now let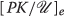
denote the equilibrium concentration established by equation 4. Then if the trigger T0 increases
by
, we see
(5)
which implies the percentage increase from equilibrium is
. This back of the envelope calculation can be done not only at step i but at the other steps as well. Letting \(\delta _{T_{1}/T_{1}^{\sim } P}\) and
denote changes in critical molecular concentrations, let’s examine the stage ii equilibrium loop. We have
(6)
The kinetic equations are then
(7)
(8)
Dynamic equilibrium then implies that
and hence
or
(9)
Equation 9 defines the equilibrium concentrations of \(\left [T_{1}/T_{1}^{\sim } P\right ]_{e}\) and
. Now if \(\left [T_{1}/T_{1}^{\sim } P\right ]\) increased to \(\left [T_{1}/T_{1}^{\sim } P\right ] \: + \: \delta _{T_{1}/T_{1}^{\sim } P}\), the percentage increase would be \(100 \: \biggl (1 \: + \: \frac {\delta _{T_{1}/T_{1}^{\sim } P}}{[T_{1}/T_{1}^{\sim } P]_{e}} \biggr)^{2}\). If the increase in \([T_{1}/T_{1}^{\sim } P]\) is due to step i, we know
We also know
and therefore
For convenience, let’s define the relative change in a variable x as \(r_{x} \: = \: \frac {\delta _{x}}{x}\). Thus, we can write
which allows us to recast the change in \(\left [T_{1}/T_{1}^{\sim }\right ]\) equation as
Hence, it follows that
and so
From this, we see that trigger events which cause
to exceed one, create an explosive increase in
. Finally, in the third step, we have
(10)
This dynamical loop can be analyzed just as we did in step ii. We see
and the triggered increase in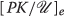
by
induces the relative change
We can therefore clearly see the multiplier effects of trigger T0 on protein production T1 which, of course, also determines changes in the production of P(T1).
The mechanism by which the trigger T0 creates activated kinase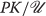
can be complex; in general, each unit of T0 creates λ units of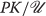
where λ is quite large – perhaps 10,000 or more times the base level of
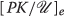. Hence, if
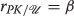and
, we have
for β>>1. From this quick analysis, we can clearly see the potentially explosive effect changes in T0 can have on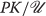
. Let us note two every important points now: there is richness to this pathway and the target P(T1) can alter hardware or software easily. If P(T1) was a K+ voltage activated gate, then we see an increase of \(\delta _{T_{1}}\) (assuming 1−1 conversion of T1 to P(T1)) in the concentration of K+ gates. This corresponds to a change in the characteristics of the axonal pulse. Similarly, P(T1) could create Na+ gates thereby creating change in axonal pulse characteristics. P(T1) could also create other proteins whose impact on the axonal pulse is through indirect means such as the kill \(T_{0}^{\prime }\) etc. pathways. There is also the positive feedback pathway via
through the T0 receptor creation. Note that all of these pathways are essentially modeled by this primitive.
Second messengers
The monoamine neurotransmitters dopamine, serotonin and norepinephrine modulate the use of Ca+2 within a cell in a variety of ways. From the discussions in (Hille 1992), the protein levels of AC, adenyl cyclase; CAMP, cyclic adenosine monophosphate; G proteins Gi, Gs, Go and Gp; PDE, phosphodiesterase; PKA, CAMP dependent kinase; CamK, calmodulin dependent kinase; PLC, phospholipase C; PKC, C kinase; IP3, inositol-1,4,5 triphosphate; DAG, diacylglycerol; IN1, PKA inhibitor; PP, generic protein phosphotase; S1, S2, S3, S4, S6 and S7, surface proteins, and others, can all be altered. Creation of these proteins alters the hardware of the cell; indeed, these proteins Si could be anything used in the functioning of the cell. Following (Bray 1998), we can infer protein kinases, protein phosphatases, transmembrane receptors etc. that carry and process messages inside the cell are associated with compact clusters of molecules attached to the cell membrane which operate as functional units and signaling complexes provide an intermediate level of organization like the integrated circuits used in VLSI. However, this interpretation is clearly flawed as these circuits are self-modifying. A close look extracellular triggers abstractly helps us understand how to approximate their effects. The full details showing how we obtain abstractions of information processing can be found in (Peterson 2014b) and here, we will be brief. Let T0 denote a second messenger trigger which moves though a port P to create a new trigger T1 some of which binds to B1. We have already discussed this is an abstract way. Here we are looking at it more computationally. A schematic of this is shown in Figure 1. In the figure, r is a number between 0 and 1 which represents the fraction of the trigger T1 which is free in the cytosol. Hence, 100r% of T1 is free and 100(1−r) is bound to B1 creating a storage complex B1/T1. For our simple model, we assume rT1 is transported to the nuclear membrane where some of it binds to the enzyme E1. Let s in (0,1) denote the fraction of rT1 that binds to E1. We illustrate this in Figure 2.
Figure 1
A second messenger trigger.
Figure 2
Some T1 binds to the genome.
We denote the complex formed by the binding of E1 and T1 by E1/T1. From Figure 2, we see that the proportion of T1 that binds to the genome (DNA) and initiates protein creation P(T1) is thus srT1.
The protein created, P(T1), could be many things. Here, let us assume that P(T1) is a sodium, Na +, gate. Thus, our high level model is sE1/rT1 + DNA→Na+ gate We therefore increase the concentration of Na + gates, [Na+] thereby creating an increases in the sodium conductance, gNa. The standard Hodgkin - Huxley conductance model (details are in (Peterson 2014c)) is given by \(g_{\textit {Na}}(t,V) = g_{\textit {Na}}^{max} \mathcal {M}_{\textit {Na}}^{p}(t,v) \mathcal {H}_{\textit {Na}}^{q}(t,V)\) where t is time and V is membrane voltage. The variables \(\mathcal {M}_{\textit {Na}}\) and \(\mathcal {H}_{\textit {Na}}\) are the activation and inactivation functions for the sodium gate with p and q appropriate positive powers. Finally, \(g_{\textit {Na}}^{max}\) is the maximum conductance possible. These models generate \(\mathcal {M}_{\textit {Na}}\) and \(\mathcal {H}_{\textit {Na}}\) values in the range (0,1) and hence, \(0 \: \leq \: g_{\textit {Na}}(t,V) \: \leq \: g_{\textit {Na}}^{max}\).
We can model increases in sodium conductances as increases in \(g_{\textit {Na}}^{max}\) with efficiency e, where e is a number between 0 and 1. We will not assume all of the sE1/rT1 + DNA to sodium gate reaction is completed. It follows that e is similar to a Michaelson - Mentin kinetics constant. We could also alter activation, \(\mathcal {M}_{\textit {Na}}\), and/or inactivation, \(\mathcal {H}_{\textit {Na}}\), as functions of voltage, V in addition to the change in the maximum conductance. However, we are interested in a simple model at present. Our full schematic is then given in Figure 3.
Figure 3
Maximum sodium conductance control pathway.
We can model the choice process, rT1 or (1−r)B1/T1 via a simple sigmoid, \(f(x) = 0.5 \left (1 + \tanh \left (\frac {x-x_{0}}{g}\right) \right)\) where the transition rate at x0 is \(f^{\prime }(x_{0}) = \frac {1}{2g}\). Hence, the “gain” of the transition can be adjusted by changing the value of g. We assume g is positive. This function can be interpreted as switching from of “low” state 0 to a high state 1 at speed \(\frac {1}{2g}\). Now the function h=rf provides an output in (r,∞). If x is larger than the threshold x0, h rapidly transitions to a high state r. On the other hand, if x is below threshold, the output remains near the low state 0.
We assume the trigger T0 does not activate the port P unless its concentrations is past some threshold [ T0]b where [ T0]b denotes the base concentration. Hence, we can model the port activity by \(h_{p}([\!T_{0}]) = \frac {r}{2} \left (~ 1 + \tanh \left (\frac {[T_{0}]-[T_{0}]_{b}}{g_{p}}\right) ~\right)\) where the two shaping parameters gp (transition rate) and [ T0]b (threshold) must be chosen. We can thus model the schematic of Figure 1 as hp([ T0]) [ T1]n where [ T1]n is the nominal concentration of the induced trigger T1. In a similar way, we let \(h_{e}(x) = \frac {s}{2}\left (~ 1 + \tanh \left (\frac {x-x_{0}}{g_{e}}\right) ~\right)\) Thus, for x = hp([ T0]) [ T1]n, we have he is a switch from 0 to s. Note that 0 ≤ x ≤ r[ T1]n and so if hp([ T0]) [ T1]n is close to r[ T1]n, he is approximately s. Further, if hp([ T0]) [ T1]n is small, we will have he is close to 0. This suggests a threshold value for he of \(\frac {r[T_{1}]_{n}}{2}\). We conclude
which lies in [0,s). This is the amount of activated T1 which reaches the genome to create the target protein P(T1). It follows then that [ P(T1)]=he(hp([ T0]) [ T1]n)[ T1]n The protein is created with efficiency e and so we model the conversion of [ P(T1)] into a change in \(g_{\textit {Na}}^{max}\) as follows. Let
which has output in [0,e). Here, we want to limit how large a change we can achieve in \(g_{\textit {Na}}^{max}\). Hence, we assume there is an upper limit which is given by \(\Delta \: g_{\textit {Na}}^{max} \: = \: \delta _{\textit {Na}} \: g_{\textit {Na}}^{max}\). Thus, we limit the change in the maximum sodium conductance to some percentage of its baseline value. It follows that hNa(x) is about δNa if x is sufficiently larges and small otherwise. This suggests that x should be [P(T1)] and since translation to P(T1) occurs no matter how low [T1] is, we can use a switch point value of x0=0. We conclude
Our model of the change in maximum sodium conductance is therefore \(\Delta \: g_{\textit {Na}}^{max} \: = \: h_{\textit {Na}}([\!P(T_{1})])\). We can thus alter the action potential via a second messenger trigger by allowing
for appropriate values of p and q within a standard Hodgkin - Huxley model.
Next, if we assume a modulatory agent acts as a trigger T0 as described above, we can generate action potential pulses using the standard Hodgkin - Huxley model for a large variety of critical sodium trigger shaping parameters. We label these with a Na to indicate their dependence on the sodium second messenger trigger. \(\left [ r^{Na}, {[\!T_{0}]_{b}}^{Na}, g^{Na}_{p}, s^{Na}, g^{Na}_{e}, e^{Na}, g_{\textit {Na}}, \delta _{\textit {Na}} \right ]^{\prime }\) We can follow the procedure outlined in this section for a variety of triggers. We therefore can add a potassium gate trigger with shaping parameters \(\left [r^{K},{[\!T_{0}]^{K}}_{b},{g^{K}_{p}}, s^{K},{g^{K}_{e}}, e^{K}, g_{K}, \delta _{K}\right ]^{\prime }\).
Concatenated sigmoid transitions:
In the previous section, we have found how to handle alterations in \(g_{\textit {Na}}^{max}\) due to a trigger T0. We have
with e and δNain (0,1). Let \(\boldsymbol {\sigma }(x,x_{0},g_{0}) = \frac {1}{2} \Biggl (1 + \tanh \biggl (\frac {x-x_{0}}{g_{0}}\biggr) \Biggr)\) Then the sodium conductance modification equation is \(h_{\textit {Na}}([P(T_{1})]) = e \delta _{\textit {Na}}g_{\textit {Na}}^{max} \boldsymbol {\sigma }([P(T_{1})], 0, g_{\textit {Na}})\). Using this same notation, we see
$$\begin{array}{@{}rcl@{}} h_{p}(\left[T-0\right]) &=& r \: \boldsymbol{\sigma}([\!T_{0}], [\!T_{0}]_{b}, g_{p})\\ h_{e}(h_{p}([\!T_{0}]) [\!T_{1}]_{n}) &=& s \: \boldsymbol{\sigma} \left (\: h_{p}([\!T_{0}])[\!T_{1}]_{n}, \frac{r[\!T_{1}]_{n}}{2}, g_{e} \right)\\ &=& s \: \boldsymbol{\sigma} \left({\vphantom{\frac{r[T_{1}]_{n}}{2}}} \: r \: \boldsymbol{\sigma} ([\!T_{0}], [\!T_{0}]_{b}, g_{p}) [\!T_{1}]_{n},\right.\\ &&\left.\frac{r[T_{1}]_{n}}{2}, g_{e} \right) \end{array} $$
Note the concatenation of the sigmoidal processing. Now [P(T1)]=he(hp([ T0])[ T1]n)[ T1]n. Thus,
$${\fontsize{9.2}{6}\begin{aligned} \left[P(T_{1})\right]= s \boldsymbol{\sigma} \left (\: r \boldsymbol{\sigma}([\!T_{0}], [\!T_{0}]_{b}, g_{p}) [\!T_{1}]_{n}, \frac{r[\!T_{1}]_{n}}{2}, g_{e} \right) [\!T_{1}]_{n}. \end{aligned}} $$
Implicit is this formula is the cascade “ σ (σ (σ” as σ([ P(T1)],0,gNa) uses two concatenated sigmoid calculations itself. We label this as a σ3 transition and use the notation
$$\begin{array}{@{}rcl@{}} \begin{array}{lll} \boldsymbol{\sigma_{3}}(&[\!T_{0}],[T_{0}]_{b}, g_{p}; & \: \text{inner most sigmoid }\\ & r ; & \: \text{scale innermost calculation by} \: r\\ & [\!T_{1}]_{n} ; & \: \text{scale again by} \: [\!T_{1}]_{n}; \: \text{this is input} \\ &&\text{ to next sigmoid}\\ & \frac{r[T_{1}]_{n}}{2}, g_{e} ; & \: \text{offset and gain of next sigmoid }\\ & s ; & \: \text{scale results by} \: s\\ & [\!T_{1}]_{n} ; & \: \text{scale again by} \: [\!T_{1}]_{n}; \: \text{this is} \:\\ &&{}[\!P(T_{1})], \: \text{input into last sigmoid}\\ & 0, g_{Na} ; & \: \text{offset and gain of last sigmoid})\\ \end{array} \end{array} $$
where gT denotes the final gain associated with the third level sigmoidal transition to create the final gate product. We can then rewrite our modulation equation as
We can also recast this model into computational graph structure. This makes it easier to see how the calculations will be performed as asynchronous agents. Consider the typical standard sigmoid transformation \(h_{p}([\!T_{0}]) = \frac {r}{2} \Biggl (~ 1 + \tanh \biggl (\frac {[T_{0}] - [T_{0}]_{b}}{g_{p}} \biggr) ~ \Biggr)\). We can draw this as a graph as is shown in Figure 4 where h denotes the standard sigmoidal state transition function.
Figure 4
The first level sigmoid graph computation.
We also have \(h_{e}(h_{p}([\!T_{0}]) \: [\!T_{1}]_{n}) = \frac {s}{2}\left (1 + {\vphantom {\left (\frac {h_{p}([T_{0}])[T_{1}]_{n} -\frac {r[T_{1}]_{n}}{2}}{g_{e}}\right)}}\right.\tanh \left.\left (\frac {h_{p}([T_{0}])[T_{1}]_{n} -\frac {r[T_{1}]_{n}}{2}}{g_{e}}\right) ~\right)\) which for a given output Y becomes
and the computation can be represented graphically by Figure 5. Finally, we have used [ P(T1)]= he(hp([ T0])[ T1]n)[ T1]n and \(h_{\textit {Na}}([\!P(T_{1})]\!)\,=\,e \delta _{\textit {Na}}g_{\textit {Na}}^{max}h([\!P(T_{1})]\!, 0, g_{\textit {Na}})\) which can be shown diagrammatically as in Figure 6.
Figure 5
Sigmoid computations second level.
Figure 6
Sigmoid computations third level.
These graphs are, of course, becoming increasingly complicated. However, they are quite useful in depicting how feedback pathways can be added to our computations. Let’s add feedback pathways to the original maximum conductance control pathway we illustrated in Figure 3. Figure 7 is equivalent to that of the computational graph of Figure 6 but shows more of the underlying cellular mechanisms.
Figure 7
Adding feedback maximum sodium conductance control pathway.
The feedback pathways are indicated by the variables ξ0 and ξ1. The feedback ξ0 is meant to suggest that some of the protein kinase T1 which is bound onto (1−r)B1/T1 is recycled (probably due to other governing cycles) back to freeT1. We show this with a line drawn back to the port P. Similarly, some of the protein kinase not used for binding to the enzyme E1, to start the protein creation process culminating in P(T1), is allowed to be freed for reuse. This is shown with the line labeled with the legend 1−ξ1 leading back to the nuclear membrane. It is clear there are many other feedback possibilities. Also the identity of the protein P(T1) is fluid. We have already discussed the cases where P(T1) can be voltage dependent gates for sodium and potassium and calcium second messenger proteins. However, there are other possibilities:
B1: thereby increasing T1 binding
T1: thereby increasing rT1 and P(T1)
E1 thereby increasing P(T1).
and so forth. We can also specialize this to the case of Ca ++ triggers, but we will not do so here.
Let’s specialize our discussion to the case of a neurotransmitter trigger. When two cells interact via a synaptic interface, the electrical signal in the pre-synaptic cell triggers a release of a neurotransmitter (NT) from the pre-synapse which crosses the synaptic cleft and then by docking to a port on the post cell, initiates a post-synaptic cellular response. The general pre-synaptic mechanism consists of several key elements: one, NT synthesis machinery so the NT can be made locally; two, receptors for NT uptake and regulation; three, enzymes that package the NT into vesicles in the pre-synapse membrane for delivery to the cleft. There are two general pre-synaptic types: monoamine and peptide. In the monoamine case, all three elements for the pre-cell response are first manufactured in the pre-cell using instructions contained in the pre-cell’s genome and shipped to the pre-synapse. Hence, the monoamine pre-synapse does not require further instructions from the pre-cell genome and response is therefore fast. The peptide pre-synapse can only manufacture a peptide neurotransmitter in the pre-cell genome; if a peptide neurotransmitter is needed, there is a lag in response time. Also, in the peptide case, there is no re-uptake pump so peptide NT can’t be reused.
On the post-synaptic side, the fast response is triggered when the bound NT/ Receptor complex initiates an immediate change in ion flux through the gate thereby altering the electrical response of the post cell membrane and hence, ultimately its action potential and spike train pattern. Examples are glutumate (excitatory) and GABA (inhibitory) neurotransmitters. The slow response occurs when the initiating NT triggers a second messenger response in the interior of the cell. When the output of one neuron is sent into the input system of another, we typically call the neuron providing the input the pre-neuron and the neuron generating the output, the post-neuron. The post-neuron’s output is a classical action potential which we will eventually approximate using a low dimensional vector called the Biological Feature Vector or BFV. The pre-neuron generates an axonal pulse which influences the release of the contents of synaptic vesicles into the fluid contained in the region between the neurons. The vesicles contain neurotransmitters. For convenience, we focus on one such neurotransmitter, labeled ζ. The ζ neurotransmitter then acts like the trigger T0 we have already discussed. It binds in some fashion to a port or gate specialized for the ζ neurotransmitter. The neurotransmitter ζ then initiates a cascade of reactions:
It passes through the gate, entering the interior of the dendrite. It then forms a complex, \(\hat {\zeta }\).
Inside the post-dendrite, \(\hat {\zeta }\) influences the passage of ions through the cable wall. For example, it may increase the passage of Na+ through the membrane of the cable thereby initiating an ESP. It could also influence the formation of a calcium current, an increase in K+ and so forth.
The influence via \(\hat {\zeta }\) can be that of a second messenger trigger.
Each neuron creates a brew of neurotransmitters specific to its type. A trigger of type T0 can thus influence the production of neurotransmitters with concomitant changes in post-neuron activity.
Methods
The abstract neuron model
It is clear neuron classes can have different trigger characteristics. First, consider the case of neurons which create the monoamine neurotransmitters. Neurons of this type in the Reticular Formation of the midbrain produce a monoamine neurotransmitter packet at the synaptic junction between the axon of the pre-neuron and the dendrite of the post-neuron. The monoamine neurotransmitter is then released into the synaptic cleft and it induces a second messenger response. The strength of this response is dependent on the BFV input from pre-neurons that form synaptic connections with the post-neuron. The strength of this input determines the strength of the monoamine trigger into the post-neuron dendrite. Let the strength for neurotransmitter ζ be given by the weighting term \(c^{\zeta }_{pre,post}\). The trigger at time t and dendrite location w on the dendritic cable is therefore
where \(d^{\zeta }_{pre,post}\) denotes the strength of the induced T1 response and \(D^{\zeta }_{1}\) is the diffusion constant of the T1 protein. This trigger will act through the usual pathway. Also, we let T2 denote the protein P(T1). T2 transcribes a protein target from the genome with efficiency e.
Note [ T2](t,w) gives the value of the protein T2 concentration at some discrete time t and spatial location w. This response can also be modulated by feedback. In this case, let ξ denote the feedback level. Then, the final response is altered to \(h_{T_{2}}^{f}\) where the superscript f denotes the feedback response and the constant ω is the strength of the feedback; we have \(h_{T_{2}}^{f}(t,w) = \omega \frac {1}{\xi } h_{T_{2}}(t,w)\) and \({[\!T_{2}]}(t,w) = h_{T_{2}}^{f}(t,w) [\!T_{2}]_{n}\). There are a large number of shaping parameters here. For example, for each neurotransmitter, we could alter the parameters due to calcium trigger diffusion. These would include \(D^{\zeta }_{0}\), the diffusion constant for the trigger, and \(D^{\zeta }_{1}\), the diffusion constant for the gate induced protein T1. In addition, transcribed proteins could alter – we know their first order quantitative effects due to our earlier analysis – \(d^{\zeta }_{pre,post}\), the strength of the T1 response, r, the fraction of T1 free, gp, the trigger gain, [T0]b, the trigger threshold concentration, s, the fraction of active T1 reaching genome, ge, the trigger gain for active T1 transition, [T1]n, the threshold for T1, [T2]n, the threshold for P(T1)=T2, \(g_{T_{2}}\), the gain for T2, ω, the feedback strength, and ξ, the feedback amount for T1=1−ξ. Note \(d^{\zeta }_{pre,post}\) could be simply \(c^{\lambda }_{pre,post}\). The neurotransmitter triggers can alter many parameters important to the creation of the BFV. For example, the maximum sodium and potassium conductances can be altered via the equation for T2. For sodium, \(\phantom {\dot {i}\!}T_{2}(t,w) = h_{T_{2}}(t,w) [T_{2}]_{n}\) becomes
There would be a similar set of equations for potassium. Finally, neurotransmitters and other second messenger triggers have delayed effects in general. So if the trigger T0 binds with a port P at time t0, the changes in protein levels P(T1) might also need to be delayed by a factor τζ.
Abstract neuron design
We can see the general structure of a typical action potential is illustrated in Figure 8.
Figure 8
Prototypical action potential.
We can use the following points on this generic action potential to construct a low dimensional feature vector of Equation 12.
where the model of the tail of the action potential is of the form Vm(t)=V3 + (V4−V3) tanh(g(t−t3)). Note that \(V_{m}^{\prime } (t_{3}) = (V_{4} - V_{3}) \: \: g\) and so if we were using real voltage data, we would approximate \(V_{m}^{\prime } (t_{3})\) by a standard finite difference. The biological feature vector therefore stores many of the important features of the action potential is a low dimensional form. We note these include
The interval [t0,t1] is the duration of the rise phase. This interval can be altered or modulated by neurotransmitter activity on the nerve cell’s membrane as well as second messenger signaling from within the cell.
The height of the pulse, V1, is an important indicator of excitation.
The time interval between the highest activation level, V1 and the lowest, V3, is closely related to spiking interval. This time interval, [t1,t3], is also amenable to alteration via neurotransmitter input.
The height of the depolarizing pulse, V4, helps determine how long it takes for the neuron to reestablish its reference voltage, V0.
The neuron voltage takes time to reach reference voltage after a spike. This is the time interval by the interval [t3,∞].
The exponential rate of increase in the time interval [t3,∞] is also very important to the regaining of nominal neuron electrophysiological characteristics.
We have shown the BFV captures the characteristics of the output pulse well enough to classify neurotransmitter inputs on the basis of how they change the BFV (Peterson and Khan 2006) and we will now use modulations of the BFV induced by second messengers in our nodal computations. The feature vector output of a neural object is due to the cumulative effect of second messenger signaling to the genome of this object which influences the action potential and thus feature vector of the object by altering its complicated mixture of ligand and voltage activated ion gates, enzymes and so forth. We can then define an algebra of output interactions that we can use in building the models. We motivate our approach using the basic Hodgkin - Huxley model which depends on a large number of parameters. Of course, more sophisticated action potential models can be used, but the standard two ion gate Hodgkin - Huxley model is sufficient for our needs here.
Using the vector ξ from Equation 12, we can construct the BVF. Note for the sigmoid tail model, we have \(V_{m}^{\prime } (t_{3}) = (V_{4} - V_{3}) \: \: g\) and we can approximate \(V_{m}^{\prime } (t_{3})\) by a standard finite difference. We pick a data point (t5,V5) that occurs after the minimum – typically we use the voltage value at the time t5 that is 5 time steps downstream from the minimum and approximate the derivative at t3 by \(V_{m}^{\prime } (t_{3}) \approx \frac {V_{5} - V_{3}}{t_{5} \: - \: t_{3}}\) The value of g is then determined to be \(g = \frac {V_{5} - V_{3}}{(V_{4} - V_{3})(t_{5} \: - \: t_{3})}\) which reflects the asymptotic nature of the hyperpolarization phase of the potential. Clearly, we can model an inhibitory pulse,mutatis mutandi.
The BFV functional form
In Figure 9, we indicated the three major portions of the biological feature vector and the particular data points chosen from the action potential which are used for the model. These are the two parabolas f1 and f2 and the sigmoid f3. The parabola f1 is treated as the two distinct pieces f11 and f12 given by
Thus, f1 consists of two joined parabolas which both have a vertex at t1. The functional form for f2 is a parabola with vertex at t3: f2(t)=a2+b2(t−t3)2 Finally, the sigmoid portion of the model is given by f3(t)=V3+(V4−V3) tanh(g(t−t3)) We have also simplified the BFV even further by dropping the explicit time point t4 and modeling the portion of the action potential after the minimum voltage by the sigmoid f3. From the data, it follows that
We conclude that a2=V3 and \(b^{2} = \frac {V_{2}-V_{3}}{(t_{2}-t_{3})^{2}}\). Hence, the functional form of the BFV model can be given by the mapping f of equation 15.
All of our parabolic models can also be written in the form \(p(t) = \pm \frac {1}{4 \beta } (t - \alpha)\) where 4β is the width of the line segment through the focus of the parabola. The models f11 and f12 point down and so use the “minus” sign while f2 uses the “plus”. By comparing our model equations with this generic parabolic equation, we find the width of the parabolas of f11, f12 and f2 is given by
We want to modulate the output of our abstract neuron model by altering the BFV. The BFV itself consists of 11 parameters, but better insight, into how alterations of the BFV introduce changes in the action potential we are creating, comes from studying changes in the mapping f given in Section “The BFV functional form”. In addition to changes in timing, t0, t1, t2 and t3, we can also consider the variations of Equation 16.
It is clear that modulatory inputs that alter the cap shape and hyperpolarization curve of the BFV functional form can have a profound effect on the information contained in the “action potential”. For example, a hypothetical neurotransmitter that alters V1 will also alter the latis rectum distance across the cap f1. Further, direct modifications to the latis rectum distance in any of the two caps f11 and f12 can induce corresponding changes in times t0, t1 and t2 and voltages V0, V1 and V2. A similar statement can be made for changes in the latis rectum of cap f2. For example, if a neurotransmitter induced a change of, say 1% in 4β11, this would imply that \(\Delta \biggl (\frac {V_{1}-V_{0}}{(t_{0}-t_{1})^{2}}\biggr) \: = \:.04 \beta _{11}^{0}\) where \(\beta _{11}^{0}\) denotes the original value of \(\beta _{11}^{0}\). Thus, to first order
Since we can do this analysis for any percentage r of \(\beta _{11}^{0}\), we can infer that a neurotransmitter that modulates the action potential by perturbing the “width” or latis rectum of the cap of f11 can do so satisfying the equation
Similar equations can be derived for the other two width parameters for caps f12 and f3. These sorts of equations give us design principles for complex neurotransmitter modulations of a BFV.
Modulation via the BFV ball and stick model
The BFV model we build consists of a dendritic system and a computational core which processes BFV input sequence to generate a BFV output. The standard Hodgkin-Huxley equations tell us
Since the BFV is structured so that the action potential has a maximum at t1 of value V1 and a minimum at t3 of value V3, we have \(V_{m}^{\prime }(t_{1}) \: = \: 0\) and \(V_{m}^{\prime }(t_{3}) \: = \: 0\). This gives
From Figure 10 and Figure 11, we see that for typical action potential simulation responses, we have m3(V1,t1)h(V1,t1) ≈ 0.35 and n4(V1,t1) ≈ 0.2. Further, m3(V3,t3)h(V3,t3) ≈ 0.01 and n4(V3,t3) ≈ 0.4.
Figure 10
The product
: Sodium Conductances during a Pulse 1100 at 3.0.
Figure 11
The product
: Potassium Conductances during a Pulse 1100 at 3.0.
We also know that as t goes to infinity, the action potential flattens and \(V_{m}^{\prime }\) approaches 0. Also, the applied current, IE is zero and so we must have
We can also assume that the area under the action potential curve from the point (t0,V0) to (t1,V1) is proportional to the incoming current applied. If VIn is the axon - hillock voltage, the impulse current applied to the axon - hillock is gInVIn where gIn is the ball stick model conductance for the soma. Thus, the approximate area under the action potential curve must match this applied current. We have \(\frac {1}{2} \: (t_{1} - t_{0}) \: (V_{1} - V_{0}) \approx g_{\textit {In}} V_{\textit {In}}\) We conclude \((t_{1} - t_{0}) = \frac {2 g_{\textit {In}} V_{\textit {In}}}{V_{1} - V_{0}}\). Thus
Also, we know that during the hyperpolarization phase, the sodium current is off and the potassium current is slowly bringing the membrane potential back to the reference voltage. Now, our BFV model does not assume that the membrane potential returns to the reference level. Instead, by using
Thus, letting u=g(t−t3), \(\frac {1}{2} = \frac {e^{2u} - 1}{e^{2u} + 1}\) and we find \( u \: = \: \frac {\ln (3)}{2}\). Solving for t, we then have \(t^{\ast } = t_{3} \: + \: \frac {\ln (3)}{2g}\). From t3 on, the Hodgkin - Huxley dynamics are
We want the values of the derivatives to match at t∗. This gives
where \(V^{\ast } \: = \: \frac {1}{2}(V_{3} + V_{4})\). Now \(g(t^{\ast }-t_{3}) \: = \: \frac {\ln (3)}{2}\) and thus we find
Next, consider the magnitude of
. We know at t∗,
is small from Figure 11. Thus, we will replace it by the value 0.01. This gives
We can see clearly from the above equation, that the dependence of g on \(g_{K}^{Max}\) and \(g_{\textit {Na}}^{max}\) is quite complicated. However, we can estimate this dependence as follows. We know that V3+V4 is about the reference voltage, −65.9mV. If we approximate V3 by the potassium battery voltage, Ek=−72.7mV and V4 by the reference voltage, we find \(\frac {V_{3} + V_{4}}{V_{4} - V_{3}} \: \approx \: \frac {-138.6}{6.8} \: = \: -20.38\) and \(\frac {1}{V_{4} - V_{3}} \: \approx \: \frac {1}{6.8} \: = \: 0.147\). Hence,
This gives \(\frac {\partial g}{\partial g_{K}^{Max}} \approx -710.1\). Equation 25 shows what our intuition tells us: if\(g_{K}^{Max}\)increases, the potassium current is stronger and the hyperpolarization phase is shortened. On the other hand, if\(g_{K}^{Max}\)decreases, the potassium current is weaker and the hyperpolarization phase is lengthened.
Multiple inputs
Consider a typical input V(t) which is determined by a BFV vector. Without loss of generality, we will focus on excitatory inputs in our discussions. The input consists of a three distinct portions. First, a parabolic cap above the equilibrium potential determined by the values (t0,V0), (t1,V1), (t2,V2). Next, the input contains half of another parabolic cap dropping below the equilibrium potential determined by the values (t2,V2) and (t3,V3). Finally, there is the hyperpolarization phase having functional form H(t) = V3+(V4−V3) tanh(g(t−t3)). Now assume two inputs arrive at the same electronic distance L. We label this inputs as A and B as is shown in Figure 12.
Figure 12
Two action potential inputs into the dendrite subsystem.
For convenience of exposition, we also assume \({t_{3}^{A}} \: < \: {t_{3}^{B}}\), as otherwise, we just reverse the roles of the variables in our arguments. In this figure, we note only the minimum points on the A and B curves. We merge these inputs into a new input VN prior to the hyperpolarization phase as follows:
This constructs the two parabolic caps of the new resultant input by averaging the caps of VA and VB. The construction of the new hyperpolarization phase is more complicated. The shape of this portion of an action potential has a profound effect on neural modulation, so it is very important to merge the two inputs in a reasonable way. The hyperpolarization phases of VA and VB are given by
For optimality, we find the parameters where \(\frac {\partial E}{\partial V_{3}}\), \(\frac {\partial E}{\partial V_{4}}\), \(\frac {\partial E}{\partial g}\) and \(\frac {\partial E}{\partial t_{3}}\) are 0. Now,
Upon simplification, we find \(0 = V_{3} - \frac {{V_{3}^{A}} + {V_{3}^{B}}}{2}\) and \(0 = V_{4} - \frac {{V_{4}^{A}} + {V_{4}^{B}}}{2}\). This leads to our choices for V3 and V4. \(V_{3} = \frac {{V_{3}^{A}} + {V_{3}^{B}}}{2}\) and \(V_{4} = \frac {{V_{4}^{A}} + {V_{4}^{B}}}{2}\) Equation 31 is also true at \(t = {t_{3}^{A}}\) and \(t = {t_{3}^{B}}\). This gives
For convenience, define \(w_{34}^{A} = \frac {{V_{4}^{A}}-{V_{3}^{A}}}{2}\) and \(w_{34}^{B} = \frac {{V_{4}^{B}}-{V_{3}^{B}}}{2}\). Then, using equation 32 and equation 33, we find
so that zA<0<zB. It seems reasonable that the optimal value of t3 should lie between \({t_{3}^{A}}\) and \({t_{3}^{B}}\). Note equations 34 precludes the solutions \(t_{3} = {t_{3}^{A}}\) or \(t_{3} = {t_{3}^{B}}\). To solve the nonlinear system for g and t3, we will approximate tanh by its first order Taylor Series expansion. This seems reasonable as we don’t expect \(g ({t_{3}^{A}} - t_{3})\) and \(g ({t_{3}^{A}} - t_{3})\) to be far from 0. This gives the approximate system
$$\begin{array}{@{}rcl@{}} g \left({t_{3}^{A}} - t_{3} \right) &\approx& z_{A} \: \text{and } g \left({t_{3}^{B}} - t_{3} \right) \approx z_{B} \end{array} $$
(35)
Using these, we find \(g = \frac {z_{B}}{{t_{3}^{B}} - t_{3}}\) and we obtain \(\frac {z_{B}}{{t_{3}^{B}} - t_{3}} \: \left ({t_{3}^{A}} - t_{3}\right) = z_{A}\). This can be simplified as follows:
Hence, we find the approximate optimal value of g is
$$\begin{array}{@{}rcl@{}} g &=& \frac{z_{B} - z_{A}}{{t_{3}^{B}} - {t_{3}^{A}}} \end{array} $$
(37)
It is easy to check that this value of t3 lies in \(\left ({t_{3}^{A}}, {t_{3}^{B}}\right)\) as we suspected it should and that g is positive. We summarize our results. Given two input BFVs, the sigmoid portions of the incoming BFVs combine into the new sigmoid given by
Given an input sequence of BFV’s into a port on the dendrite of an accepting neuron {Vn,Vn−1,…,V1} the procedure discussed above computes the combined response that enters that port at a particular time. The inputs into the dendritic system are combined pairwise; V2 and V1 combine into a Vnew which then combines with V3 and so on. We can do this at each electrotonic location.
Pre-neurons can supply input to the dendrite cable at electronic positions w=0 to w=4. These inputs generate an ESP or ISP via many possible mechanisms or they alter the structure of the dendrite cable itself by the transcription of proteins. The output of a pre-neuron is a BFV which must then be associated with an abstract trigger as we have discussed in earlier chapters. The strength of a BFV output will be estimated as follows: The area under the first parabolic cap of the BFV can be approximated by the area of the triangle, A, formed by the vertices (t0,V0),(t1,V1),(t2,V2). This area is shown in Figure 13. The area is given by \(A = \frac {1}{2}(V_{2} -V_{0})(t_{2} - t_{0})\).
Figure 13
The EPS triangle approximation.
The size of this area then allows us to determine the first and second messenger contributions this input makes to the post-neuron.
Results and discussion
In Erlang, (Armstrong 2013), the fundamental unit of calculation in the process. Each process does not share information with any other process and hence, the memory model followed is based on message passing. There are other approaches such as shared memory with locks, software transactional memory (used in Clojure) and futures and promises. We focus on Erlang’s model as we feel a neuron in a brain model is a computational unit which performs a calculation on the basis of current inputs (i.e. messages) and sends its output to other nodes based on its forward link set. In Erlang, the message passing is asynchronous (as is the case in the BFV outputs a brain model’s node sends out to its recipients) and hence data must be copied for the message. Hence, since we want to have many node and edge functions in the brain model, \(\boldsymbol {\mathcal {G}(N,E)}\), it is important to keep the amount of calculation in each node and edge low. To achieve that, we need to approximate the neuronal calculations as we have been discussing here. Instead of solving systems of ordinary or partial differential equations are each node, we have found approximations to the solutions which capture a reasonable amount of the information processing complexity that is there. Also, the approach we use allows us to pay close attention to the architectural skeleton given by the graph \(\boldsymbol {\mathcal {G}(N,E)}\) and separate the processing function from it. Another approach is to use a middle ware tool such as CORBA implemented in C ++ using omniORB-4.1.4 to handle multiple core/ multiple CPU models, but the functional programming approach using Erlang with no shared memory is better suited to this task. In addition, we want the model to be able to use both first and second messenger triggers even though the second messenger inputs alter the computational abilities of the node they effect. We handle this by allowing the second messenger triggers to alter the low dimensional BFV. To indicate how this would be done, let’s consider a model with neurons that are first messenger types (i.e. alter the sodium and potassium gate parameters in our simple standard Hodgkin-Huxley model) and two additional neuron types that generate second messenger triggers such as dopamine and serotonin. Let’s call these classes NF, ND and NS, We are aware the situation is much more complicated but this simple thought experiment will show how our approximations are used. Consider a node N=yi in the graph and recall we are using the general update strategy given by
where each σ represents a nodal process and each Ej→i an edge process as modeled in Erlang with y denoting the input to a node and Y, the output from the node.
When the process that handles this node looks at its input queue, it sees messages M organized into the families MF, MD and MS. We use the combining inputs algorithm to merge multiple inputs in each message class into one input which we will denote by IF, ID and S.
The inputs IF, ID and S then generate an trigger update using the EPS/ IPS triangle approximation. given by aF, aD, and aS. The latter two are second messengers. Recall, a second messenger trigger T creates activated kinase
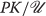and each unit of T creates λ units of
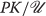where λ is quite large – perhaps 10,000 or more times the base level of
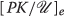. Thus, letting
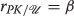and
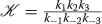, we know
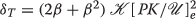. Denote the actual trigger updates by δF, δD, and δS. Hence, we can model each of the two second messenger trigger changes as
From our discussion of how the BFV is altered by triggers given in Section “Modulation of the BFV parameters”, it is clear a second messenger trigger update initiates changes in the BFV. The literature on the effects a neurotransmitter has on the action potential of an excitable neuron gives us specific information about what parts of the action potential are changed. We do not discuss these details here for brevity. Suffice it to say, we can assign each neurotransmitter to a BVF alteration. Thus, letting the proportionality constants above be KD and KS
where the gradients here are the specific changes in the 11 parameters of the BFV that each neurotransmitter causes. Also, recall the efficacy of the second messenger release depends ru, the rate of re-uptake in the connection between two nodes, the second messenger destruction rate rd, the rate of second messenger release, rr and the density of the second messenger receptor, nd. The triple (ru,rd,rr)) thus determines a net increase or decrease of second messenger concentration between two nodes: rr−ru−rd≡rnet. The efficacy of a connection between nodes is then proportional to the product rnet×nd. The density of the second messenger receptor is amenable to second messenger alterations via triggers as well. If we change our update equations to
by absorbing the nd term into the proportionality constants, we have a mechanism that allows us to model neurotransmitter interaction in the synaptic cleft.
For the input IF which is a first messenger type, we know this will cause a change in maximum sodium or potassium conductance and perhaps more complicated combinations. These were explored in Section “Modulation of the BFV parameters”. For example, we can estimate how the parameter V1 of the BFV changes via
is a reasonable approximation to this alteration of the BFV due to this first messenger input.
Hence, our processing node handles the messages in its input queue using simple arithmetic and a few stored parameters. Each edge process computes the rnet term required but it is still simpler as it only has to connect the BFV from one neuron to another.
Conclusions
We have shown how to approximate neuronal computation for both first and second messenger systems so that a graph model \(\boldsymbol {\mathcal {G}(N,E)}\) can be implemented efficiently in a modern functional programming language such as Erlang. Other languages are possible but our focus was on Erlang alone here. The simulation of a brain model then can take advantage of as many cores as are available on our hardware. Erlang is not designed for heavy computation, so this is why we have spent so much time discussing ways to approximate neural computations at each node and the synaptic processing. It is important to note that new and interesting simulations require us to pay much closer attention to the actual hardware we will be using. Hence, while the details of the multicore use might change with new hardware, the basic principles of how we combine computational algorithms to hardware via software will be retained.
Declarations
Authors’ Affiliations
(1)
Department of Biological Sciences, Department of Mathematical Sciences, Clemson University
References
Armstrong, J. (2013). Programming Erlang Second Edition: Software for a Concurrent World. Dallas, TX: The Pragmatic Bookshelf.Google Scholar
Bray, D (1998). Signalling complexes: Biophysical constraints on intracellular communication. Annual Review of Biophysics and Biomolecular Structure, 27, 59–75.View ArticleGoogle Scholar
Friston, K (2005). A theory of cortical responses. Philosophical Transactions of the Royal Society B, 360, 815–836.View ArticleGoogle Scholar
Friston, K (2010). The free-energy principle: a unified brain theory?Nature Reviews: Neuroscience, 11, 127–138.View ArticleGoogle Scholar
Gerhart, J, & Kirschner, M. (1997). Cells, Embryos and Evolution: Towards a Cellular and Developmental Understanding of Phenotypic Variation and Evolutionary Adaptability. USA: Blackwell Science.Google Scholar
Hille, B. (1992). Ionic Channels of Excitable Membranes. New York: Sinauer Associates Inc.Google Scholar
Li, X, Xia, S, Bertish, H, Branch, C, DeLisi, L (2012). Unique topology of language processing brain network: A systems-level biomarker of schizophrenia. Schizophrenia Research, 141, 128–136.View ArticleGoogle Scholar
Maia, T, & Frank, M (2011). From reinforcement learning models to psychiatric and neurological disorders. Nature Neuroscience, 14(2), 154–162.View ArticleGoogle Scholar
Peterson, J (2014a). Computation in networks. Computational Cognitive Science. This issue.Google Scholar
Peterson, J (2014b). BioInformation Processing, A Primer on Computational Cognitive Science. In Preparation, Cognitive Science and Technology Series. Springer, Singapore.Google Scholar
Peterson, J (2014c). Calculus for Cognitive Scientists: Partial Differential Equation Models. In Preparation, Cognitive Science and Technology Series. Springer, Singapore.Google Scholar
Peterson, J, & Khan, T (2006). Abstract action potential models for toxin recognition. Journal of Theoretical Medicine, 6(4), 199–234.MathSciNetView ArticleGoogle Scholar
Russo, S, & Nestler, E (2013). The brain reward circuitry in mood disorders. Nature Reviews: Neuroscience, 14, 609–625.View ArticleGoogle Scholar
Sherman, S (2004). Interneurons and triadic circuitry of the thalamus. Trends in Neuroscience, 27(11), 670–675.View ArticleGoogle Scholar
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited.
which captures the connectivity or topology of the brain model on top of which is laid the instructions for information processing via the time dependent node and edge processing functions. A simple look at edge processing shows the nodal output which is perhaps an action potential which is transferred without change to a synaptic connection where it initiates a spike in C
a
+2 ions which results in neurotransmitter release. The efficacy of this release depends on many things, but we can focus on four: r
u
(i,j), the rate of re-uptake of neurotransmitter in the connection between node N
i
and node N
j
; the neurotransmitter is destroyed via an appropriate oxidase at the rate r
d
(i,j); the rate of neurotransmitter release, r
r
(i,j) and the density of the neurotransmitter receptor, n
d
(i,j). The triple (r
u
(i,j),r
d
(i,j),r
r
(i,j))≡T(i,j) determines a net increase or decrease of neurotransmitter concentration between the two nodes: r
r
(i,j)−r
u
(i,j)−r
d
(i,j)≡r
net
(i,j). The efficacy of a connection between nodes is then proportional to the product W
i,j
=r
net
(i,j)×n
d
(i,j). Hence, each triple is a determining signature for a given neurotransmitter and the effectiveness of the neurotransmitter is proportional to the new neurotransmitter flow times the available receptor density. A very simple version of this is to simply assign the value of the edge processing function E
j→i
to be the weight W
i,j
as is standard in a simple connectionist architecture. We want to be more sophisticated than this and therefore want to allow our nodal processing functions to approximate the effects of both first and second messenger systems; consult (Peterson 2014a) for more detail.
to form the complex
. This chain of events looks like this:
where CSR denotes a cell surface receptor.
where \(T_{1}^{\sim } P\) denotes the phosphorylated version of \(T_{1}^{\sim }\). Since T
1 is bound into the complex \(T_{1}/T_{1}^{\sim }\), we actually have
In the cell, there is always present a collection of proteins which tend to bond with the phosphorylated form \(T_{1}^{\sim } P\). Such a system is called a tagging system. The protein used by the tagging system is denoted by
and usually a chain of n such
. The tagging system creates the new complex
. This gives the following event tree at this point:
, it would work just as well on
where Q is any other tagged protein. We will denote the removal system which destroys
. This symbol means the system acts on
units and outputs S via mechanism f. Note the details of the mechanism f are largely irrelevant here. Thus, we have the reaction
which releases T
1 into the cytoplasm. The full event chain is thus:
will also block transcription.
where the step i, step ii and step iii can be inhibited as shown below:
Note we have expanded to a system of four triggers which effect the outcome of P(T
1). Also, note that step i is a phosphorylation step. Now, let’s refine our analysis a bit more. Usually, reactions are paired: we typically have the competing reactions
Hence, we can imagine that step i is a system which is in dynamic equilibrium. The amount of \(T_{1}/T_{1}^{\sim } P\) formed and destroyed forms a stable loop with no net \(T_{1}/T_{1}^{\sim } P\) formed. The trigger T
0 introduces additional
where k
1 and k
−1 are the forward and backward reaction rate constants and we assume the amount of \(T_{1}/T_{1}^{\sim }\) inside the cell is constant and maintained at the equilibrium concentration \(\left [T_{1}/T_{1}^{\sim }\right ]_{e}\). Since one unit of
combines with one unit of \(T_{1}/T_{1}^{\sim }\) to phosphorylate \(T_{1}/T_{1}^{\sim }\) to \(T_{1}/T_{1}^{\sim } P\), we see
where k
1 and k
−1 are the forward and backward reaction rate constants and we assume the amount of \(T_{1}/T_{1}^{\sim }\) inside the cell is constant and maintained at the equilibrium concentration \(\left [T_{1}/T_{1}^{\sim }\right ]_{e}\). Since one unit of
. For this reaction, we have
; thus, we find
. For this reaction, we have
; thus, we find
denote the equilibrium concentration established by equation 4. Then if the trigger T
0 increases
by
, we see
denote the equilibrium concentration established by equation 4. Then if the trigger T
0 increases
by
, we see
. This back of the envelope calculation can be done not only at step i but at the other steps as well. Letting \(\delta _{T_{1}/T_{1}^{\sim } P}\) and
denote changes in critical molecular concentrations, let’s examine the stage ii equilibrium loop. We have
. This back of the envelope calculation can be done not only at step i but at the other steps as well. Letting \(\delta _{T_{1}/T_{1}^{\sim } P}\) and
denote changes in critical molecular concentrations, let’s examine the stage ii equilibrium loop. We have
and hence
or
and hence
or
. Now if \(\left [T_{1}/T_{1}^{\sim } P\right ]\) increased to \(\left [T_{1}/T_{1}^{\sim } P\right ] \: + \: \delta _{T_{1}/T_{1}^{\sim } P}\), the percentage increase would be \(100 \: \biggl (1 \: + \: \frac {\delta _{T_{1}/T_{1}^{\sim } P}}{[T_{1}/T_{1}^{\sim } P]_{e}} \biggr)^{2}\). If the increase in \([T_{1}/T_{1}^{\sim } P]\) is due to step i, we know
and therefore
and so
to exceed one, create an explosive increase in
. Finally, in the third step, we have
to exceed one, create an explosive increase in
. Finally, in the third step, we have
and
, we have
: Sodium Conductances during a Pulse 1100 at 3.0.
: Potassium Conductances during a Pulse 1100 at 3.0.
and
be denoted by
and
for simplicity of exposition,
and
, we have
We see
and
, we have
. We know at t
∗,
is small from Figure 11. Thus, we will replace it by the value 0.01. This gives
. We know at t
∗,
is small from Figure 11. Thus, we will replace it by the value 0.01. This gives
and
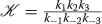, we know
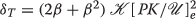. Denote the actual trigger updates by δ
F
, δ
D
, and δ
S
. Hence, we can model each of the two second messenger trigger changes as
$$\begin{array}{@{}rcl@{}} \boldsymbol{\delta_{D}} &\propto& (2 \beta_{D} + {\beta_{D}^{2}}) \boldsymbol{a_{D}} ~\text{and}~ \boldsymbol{\delta_{S}} \propto (2 \beta_{S} + {\beta_{S}^{2}}) \boldsymbol{a_{S}}. \end{array} $$From our discussion of how the BFV is altered by triggers given in Section “Modulation of the BFV parameters”, it is clear a second messenger trigger update initiates changes in the BFV. The literature on the effects a neurotransmitter has on the action potential of an excitable neuron gives us specific information about what parts of the action potential are changed. We do not discuss these details here for brevity. Suffice it to say, we can assign each neurotransmitter to a BVF alteration. Thus, letting the proportionality constants above be K D and K S$$\begin{array}{@{}rcl@{}} \boldsymbol{\delta_{D}} &=& \left(2 \beta_{D} + {\beta_{D}^{2}}\right) \boldsymbol{a_{D}} \boldsymbol{K_{D}} \: \Longrightarrow \: \nabla_{D}(BFV)\\ \boldsymbol{\delta_{S}} &=& \left(2 \beta_{S} + {\beta_{S}^{2}}\right) \boldsymbol{a_{S}} \boldsymbol{K_{S}} \: \Longrightarrow \: \nabla_{S}(BFV) \end{array} $$where the gradients here are the specific changes in the 11 parameters of the BFV that each neurotransmitter causes. Also, recall the efficacy of the second messenger release depends r u , the rate of re-uptake in the connection between two nodes, the second messenger destruction rate r d , the rate of second messenger release, r r and the density of the second messenger receptor, n d . The triple (r u ,r d ,r r )) thus determines a net increase or decrease of second messenger concentration between two nodes: r r −r u −r d ≡r net . The efficacy of a connection between nodes is then proportional to the product r net ×n d . The density of the second messenger receptor is amenable to second messenger alterations via triggers as well. If we change our update equations to$$\begin{array}{@{}rcl@{}} \boldsymbol{\delta_{D}} &=& (r_{r} - r_{u} - r_{d}) \: \left(2 \beta_{D} + {\beta_{D}^{2}}\right) \boldsymbol{a_{D}} \boldsymbol{K_{D}}\\ \boldsymbol{\delta_{S}} &=& \left(2 \beta_{S} + {\beta_{S}^{2}}\right) \boldsymbol{a_{S}} \boldsymbol{K_{D}}. \end{array} $$
